数据结构
二叉查找树
二叉搜索树(又叫二叉查找树),它是具有下列性质的二叉树:
若左子树不空,则左子树上所有结点的值均小于它的根结点的值; 若右子树不空,则右子树上所有结点的值均大于或等于它的根结点的值; 左、右子树也分别为二叉搜索树。
总之:二叉搜索树中,左子树都比其根节点小,右子树都比其根节点大,递归定义。
二叉搜索树的中序遍历一定是从小到大排序的。
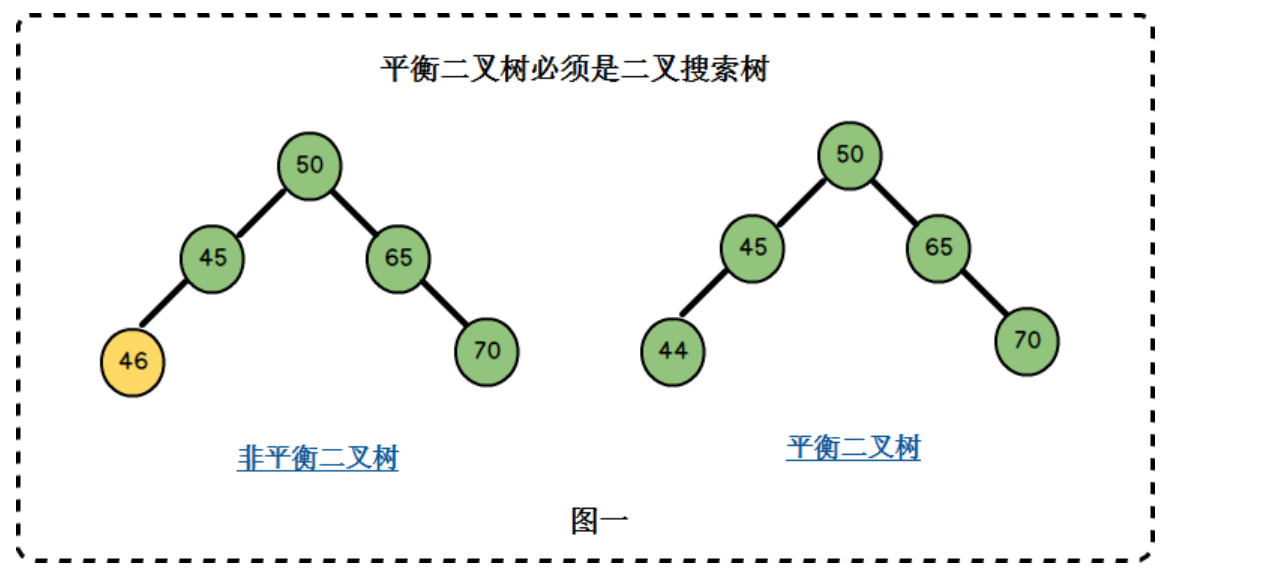
平衡二叉树
它或者是一颗空树,或它的左子树和右子树的深度之差(平衡因子)的绝对值不超过1,且它的左子树和右子树都是一颗平衡二叉树。
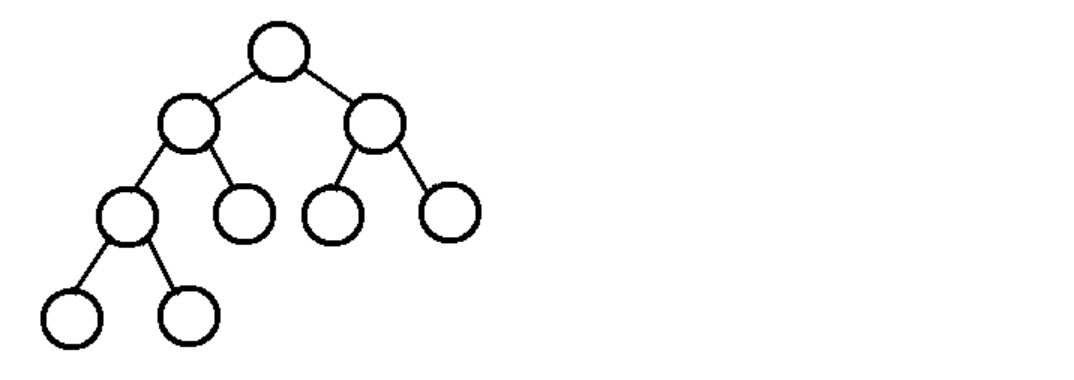
完全二叉树
若设二叉树的深度为k,除第 k 层外,其它各层 (1~k-1) 的结点数都达到最大个数,第k 层所有的结点都连续集中在最左边,这就是完全二叉树。
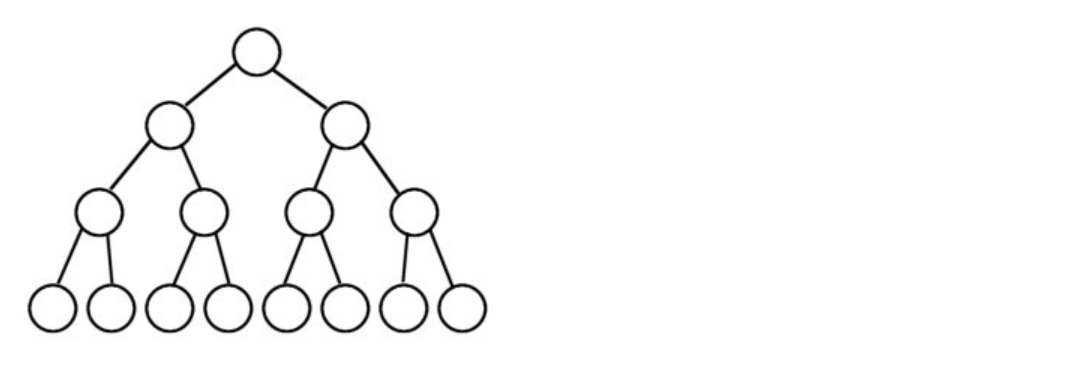
满二叉树
一棵二叉树的结点要么是叶子结点,要么它有两个子结点(如果一个二叉树的层数为K,且结点总数是(2^k) -1,则它就是满二叉树。)
红黑树
红黑树是一种自平衡的二叉查找树,它具有这些特点:
- 根节点是黑色
- 节点是红色或黑色
- 每个叶子节点都是黑色的空节点
- 每个红色的节点,它的两个子节点都是黑色。(从每个叶子到根的路径上不能有两个连续的红色节点)
- 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点
正是因为这些规则特点,使得红黑树从根到叶子的最长路径不会超过最短路径的 2 倍。
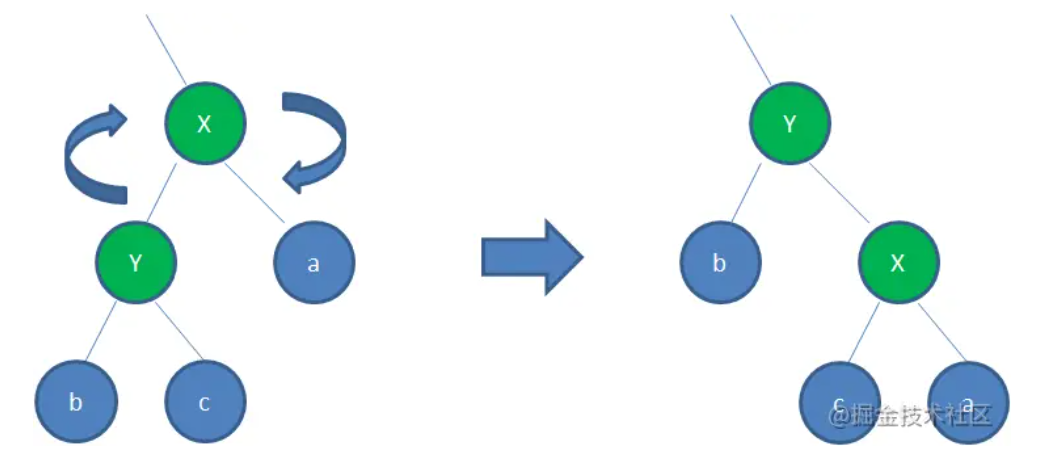
节点的旋转
左旋转:父节点变成右孩子的左孩子,原本的右孩子变成自己的父节点。
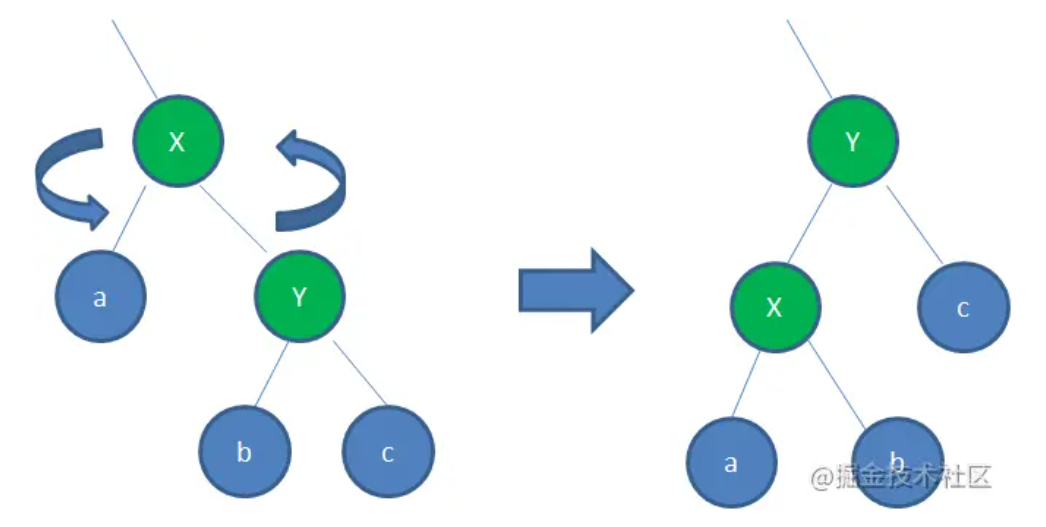
右旋转:父节点变成左孩子的右孩子,原本的左孩子变成自己的父节点。
B树和B+树
B树和B+树详解 - 51life - 博客园 (cnblogs.com)
数据结构 4 时间复杂度、B-树 B+树 具体应用与理解 - 程序猿小码 - 博客园 (cnblogs.com)
B+树的特点
- 有K个子节点的中间节点包含有K个元素,(B树这里是k-1),中间节点的元素不保存数据,只用来索引,所有的数据都保存在叶子节点。
- 所有的叶子节点包含了全部的元素信息。叶子节点本身按照关键词的大小自小而大顺序排列。
- 所有的中间节点元素都同时存在于子节点中。在子节点元素中是最大或者最小的元素。
